Lab 4: The Craft of Training Networks
Today's lab will look at the learning rate and momentum parameters, and we will consider some of the pragmatic issues that arise in training networks. As we will see, there is often much trial and error in training networks. Even for the simple networks we are using, there may be no obvious answer to such basic questions as "how many units should the hidden layer have", or which parameters (learning rate and momentum) to use.
A further goal of today's lab is to explore the hidden representations developed by the network as it learns. For this purpose, we will learn how to analyse the hidden unit activation patterns associated with each input pattern to see what similarities the netork is using to solve the task.
We will use a new problem today, as illustrated in the table below. First, create a 4x3x1 network. The patterns to be used first are in the file "duoFull.pat". The network's task is to learn to categorize these patterns into two classes. It should generate a 1 at the output if and only if there are exactly two units "on" in the input. Otherwise, it should generate a 0.
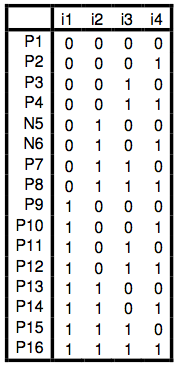
Consider the task yourself first. Why is this difficult? What makes patterns of the one class more similar to each other than to patterns of the other class? Can the network make use of the same characteristics of the data as you can?
Now train the network. You should try various values of the learning rate, of momentum, and then you should vary the number of units in the hidden layer. Can you do this with 2 units? With 1?
What is the effect of momentum? Does it always help? Do momentum and learning rate interact at all? When you have made your mind up about this, go back to a 2-2-1 network, load in XOR, and see if learning rate and momentum interact in the same way for that problem.
Generalization
We now wish to address the question of generalization. If you had learned to distinguish black swans from white swans on the basis of a few examples, it is reasonable to suggest that your training would generalize well to future swans, as yet unseen. You will now train a 4-3-1 network on most of the above patterns, but omitting one positive and one negative example (marked N5 and N6 in the figure above). These are available in the file "duoPart.pat".
Train the network on the partial set. Then load in duoFull.pat, and use "patterns→Show Patterns and Outputs" to see how the network fares on the two unseen patterns. (On some windows machines, this function may not work. An alternative is to select each of the new patterns individually and "test one".) Does it get them right?
Repeat. See if you can find networks that do and that don't generalize. Can you tell anything about the difference between the two kinds of solutions? Save the weights for each qualitatively different solution you find. If possible save weights for a netowrk that generalises correctly to both patterns, to only one pattern (and remember which) and to none of the patters. It may take a bit of trial and error to find these variants.
Part 2: Analysing the hidden unit representations
You should now have avaiable to you weights for networks that have arrived at qualitatively different solutions to the problem. Let's explore what the set of input patterns look like at the hidden layers. It is the representations at the hidden layer that form the basis for the performance of the network in classifying patterns.
Begin with some pencil and paper. Make 3 columns: In one, list the patterns that have less than 2 bits set to 1. In the next, lsit the patterns that have exactly 2 bits on (these should produce a "1" at the output.) In the third, list those patterns that have more than 2 bits.
Now repeat the following: Load in the weights for a network with a known behaviour. Load in the full set of patterns. Use the utulity "Hierarchical tree" to examine the hidden unit representations (that's "Layer 2"). Does the grouping you see make sense, in light of the network's ability to generalise or not? Do this for all the weights you have saved. Explore further.
