Reber Grammer
Consider the following string generator, known as a Reber grammar:
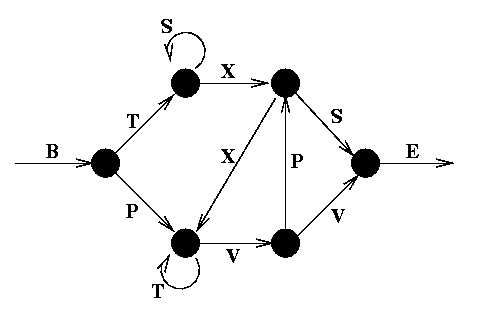 (Fig.
1)
(Fig.
1)We start at B, and move from one node to the next, adding the symbols we pass to our string as we go. When we reach the final E, we stop. If there are two paths we can take, e.g. after T we can go to either S or X, we randomly choose one (with equal probability). In this manner we can generate an infinite number of strings which belong to the rather peculiar Reber language. Verify for yourself that the strings on the left below are possible Reber strings, while those on the right are not.
| "Reber" | "Non-Reber" |
|---|---|
| BTSSXXTVVE | BTSSPXSE |
| BPVVE | BPTVVB |
| BTXXVPSE | BTXXVVSE |
| BPVPXVPXVPXVVE | BPVSPSE |
| BTSXXVPSE | BTSSSE |
What are the set of symbols which can "legally" follow a T?. An S can follow a T, but only if the immediately preceding symbol was a B. A V or a T can follow a T, but only if the symbol immediately preceding it was either a T or a P. In order to know what symbol sequences are legal, therefore, any system which recognizes reber strings must have some form of memory, which can use not only the current input, but also fairly recent history in making a decision.
The Reber grammar is an example of a simple finite state grammar and it has served as a benchmark for equally simple learning systems. A simple recurrent network can learn this grammar.
Your task is to train a Simple Recurrent Network to predict the next symbol in a sequence generated by the above grammar. If we regard 'prediction' as the task of the network, then this task is not perfectly solvable. E.g., after seeing BTS... the next symbol is not predictable, but the only two candidates are S and X, so both should be predicted in equal measure, and no other should be predicted. In a different context, e.g. after seeing BTXS, the only candidate symbol is an E. The system needs to know more than just the last symbol (S in this example).
However, if we regard the job of the network to be one of grammar induction, that is, to learn the transition probabilities in the grammar, then it can be well learned. You will need to be aware that although you are training it to do predictions, you really want it to learn the underlying grammar. Bear in mind also that the probabilities of the grammar are only imperfectly realized in the finite set of training data you have available.
Here is a file which contains a long set of reber grammar sequences: ReberInput.txt.
Using this translation, I have turned that sequence into a pattern file suitable for use in the simulator: reber.pat. The target for each symbol is simply the next symbol in the sequence. I have deliberately not placed resets at the end of each sequence. The network will simply see an unbroken stream of inputs, and will have to learn structure, including end of sequence features, itself.
Train a 7*10*7 SRN on these patterns. You will not get perfect performance, because perfect performance is, in principle, impossible. However, you should be able to evaluate the performance of the trained network.
Your mission: Train the network as well as you can. Examine the performance of the trained network. Does it always do well? Where do its predictions differ from those to be expected on the basis of the grammar itself? Why might its predictions be poorer for some transitions than others?
Treat this again as an exercise in communication. I want to know if you have understood the task, and if you understand what the network is doing, and what the network, in the best of all possible worlds, might do. Use any analysis tools you like, including the simulator, R, and anything else that you have available to you.
Hard copy answers, with an e-copy as backup, please by Friday, May 4th, 2018. Take care to use proper English, and to present your work and argumentation in a coherent manner. Use graphics judiciously. (Tips based on this book.)
If you are struggling with this, consider this table, which is only partially complete. It might help.
